Циклический алгоритм – описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Перечень повторяющихся действий называют телом цикла.
Циклические алгоритмы бывают двух типов:
Циклы со счетчиком, в которых какие-то действия выполняются определенное число раз;
Циклы с условием, в которых тело цикла выполняется, в зависимости от какого-либо условия.
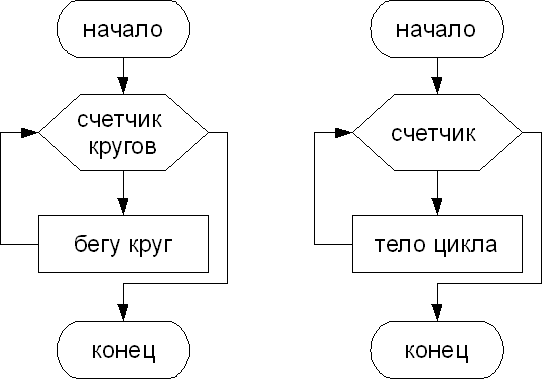
В общем случае схема циклического алгоритма со счетчиком будет выглядеть так:
Для счетчика от нач. значения до кон. значения выполнить действие. Часто бывает так, что необходимо повторить тело цикла, но заранее не известно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия. Такие циклы называются циклы с условием. Циклы в которых сначала проверяется условие, а затем, возможно, выполняется тело цикла называют циклы с предусловием. Если условие проверяется после первого выполнения тела цикла, то циклы называются циклы с постусловием.


Например, в субботу вечером вы смотрите телевизор. Время от времени поглядываете на часы и если время меньше полуночи, то продолжаете смотреть телевизор, если это не так, то вы прекращаете просмотр телепередач.


В общем случае схема циклического алгоритма с условием будет выглядеть так:
Пока условие повторять действие. При составлении циклических алгоритмов важно думать о том, чтобы цикл был конечным. Ситуация, при которой выполнение цикла никогда не заканчивается, называется зацикливанием .
Источник
Циклические структуры
Алгоритм циклической структуры – это алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий. На практике часто встречаются задачи, в которых одно или несколько действий бывает необходимо повторить несколько раз.
Многократное повторение последовательности действий называется циклом, а многократно повторяющиеся действия – телом цикла.
Изучение циклов демонстрирует учащимся главное преимущество компьютера перед человеком – выполнение большого числа действий за короткое время. Ведь даже весьма короткий циклический алгоритм, составить который не так уж долго, при исполнении может потребовать выполнения нескольких сотен действий, с которыми компьютер справится намного быстрее, чем человек.
Учащиеся должны уметь организовать цикл и верно определить тело цикла. Более того, при конструировании алгоритмов важно использовать такую конструкцию цикла, которая окажется оптимальной для решения поставленной задачи.
Существует три формы циклов: цикл с параметром, цикл с предусловием, цикл с постусловием. Каждая форма имеет стандартное описание на языке схем, а также соответствующий оператор алгоритмического языка.

а), б) – циклическая структура “Для каждого”
в) – циклическая структура “Пока”
г) – циклическая структура “До”
I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла.
1. Цикл “Для каждого” можно записать в следующем виде:
Для каждого I от A до B с шагом С:
I – счетчик числа повторов, C – приращение счетчика, A – начальное значение счетчика, B – конечное значение счетчика, P – тело цикла.
Турбо-Паскаль
2. Цикл “Пока” можно записать так:
Q – условие. ЭВМ будет выполнять P до тех пор, пока условие Q истинно.
Турбо-Паскаль
3. Цикл “До” записывается следующим образом:
Турбо-Паскаль
Тело цикла P выполняется до тех пор, пока условие Q ложно.
Одним из самых распространенных в практике вычислений алгоритмом циклической структуры является алгоритм вычислений некоторой функции y=f(x) для значений x, которые меняются от начального значения x0 до конечного xk с шагом h.
Исходными данными алгоритма являются значения: x0, xk, h. Необходимо вычисления по формуле y=f(x) повторять (xk-x0)/h+1 раз, т. е. при построении алгоритма организовать цикл. Параметром цикла выберем переменную x.
Схема алгоритма решения этой задачи на рис. 2. В схеме блок 3 присваивает начальное значение параметру цикла x, блок 6 осуществляет изменение на h параметра x при каждом выполнении цикла, блок 7 управляет циклом, для чего проверяется условие повторения цикла x 3.02.2005
Источник
С повторяющимися действиями мы сталкиваемся и в обычной жизни и при решении задач. Проход стрелок часов каждую минуту, секунду, час, смена дня и ночи, ежедневные сборы в школу, еженедельная смена уроков, ежегодные поездки на море – примеров циклов повторения миллиарды. Несмотря на разнообразие происходящих процессов, большинство из них можно описать простыми конструкциями. Делая что-то раз за разом, мы не задумываемся, что ученые уже написали алгоритмы с повторением или циклы универсальными способами.
Циклы, их виды
Многие операции, действия выполняются однотипно много раз. Этот процесс повторения называют циклом, а повторяемая последовательность – телом цикла. Процедуру с повторяющимися этапами называют циклической.
Каждое повторение действий в алгоритмах – итерация.
Выделяют 3 основных вида повторяющихся структур:
- с условием выполнения цикла (предусловием);
- с критерием завершения (постусловием);
- с указанным числом повторений цикла.
Описывать подобные процессы удобно схематично или при помощи команд.
Цикл с предусловием
Данную конструкцию еще встречается как «цикл-пока», потому что пока выполняется условием, программа/исполнитель будет проходить шаги снова и снова.Описанный критерий, логическое сравнение — причина начала прохождения повторяемых шагов/команд.
Описание цикла с условием двумя способами:
- Проверка критерия/логического сравнения.
- Пока результат «Да», «проигрывать по кругу» однотипные операции.
- Если ответ на условие отрицательный, закончить процедуру.
Особенность этой конструкции – существуют такие условия, когда команды не будут выполнены ни разу.
Циклический алгоритм, примеры:
- Написать алгоритм постройки забора из кирпичей высотой 2 м.
нц пока есть кирпичи и раствор цемента
если высота забора 1 алгоритм
Источник
Блок-схема циклического алгоритма
Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма.
Различают циклы с наперед известным и наперед неизвестным количеством проходов.
Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, …, сумма которых больше числа К.
Блок-схема алгоритма решения этой задачи приведена на рисунке 1. Она состоит из восьми блоков.
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5.
В нем при выполнении команды S = S + i производится сложение содержимого ячеек S и i, а результат записывается в ячейку S. Поскольку до операции сложения было S = 0, i = 1, то после операции будет S = 1. При записи нового значения старое содержимое ячейки S (нуль) стирается, а на его место записывается число 1.
Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.
После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К.
Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла.
Далее производится переход к блоку 7, где отпечатается значение количества членов ряда (извлечено и отпечатано число из ячейки i, которое там хранится в момент выполнения условия), суммы S и в блоке 8 алгоритм закончит работу.
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N ( под длиной массива понимается количество его элементов ). Блок-схема алгоритма дана на рисунке 2.
Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается одна константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – Z.
Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда самое N еще не известно (оно будет введено позже Z). Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к дальнейшему накоплению необходимой суммы.
Блоки 4-6 представляет собой сам цикл, в котором накапливается сумма.
Для того чтобы понять, как функционирует не только этот, а и любой другой цикл, обратимся к рисункам 3 и 4. На них показана общая структура цикла и его важнейшие параметры.
Как видно из рисунка 3, цикл состоит из заголовка и тела. Всякий цикл обязательно имеет свой счетчик.
На рисунке 4, где показана структура и параметры заголовка цикла, роль такого счетчика выполняет переменная i.
Внутри заголовка после счетчика и символа «=» через запятую указывает начальное и конечное значения счетчика и шаг его изменения (на рисунке 4 их роль выполняют переменные j, k, l соответственно). Если значение шага l = l, то его можно не указывать.
Сначала производится вход в цикл. После этого начинается его выполнение.
Внутри заголовка счетчику первоначально присваивается значение i = j. Затем выполняется блоки, образующие тело цикла. Обработка блоков внутри цикла производится по часовой стрелке. В результате после первого выполнения тела цикла управление вновь передается заголовку. Здесь к текущему значению счетчика добавится шаг. Теперь, если новое значение счетчика не вышло за свои пределы (т. е. не стало больше своего конечного значения при положительном шаге или меньше конечного значения – при отрицательном шаге), то снова выполняется тело цикла, вновь после возврата к заголовку к счетчику добавляется шаг. Так цикл будет выполняться до тех пор, пока значение счетчика однажды не выйдет за предписанный предел. Как только такой предел будет преодолен, произойдет выход из цикла и управление будет передано блоку, который следует сразу за циклом.
Вернемся к блок-схеме рис. 2. Заголовок ее цикла представлен блоком 4. Роль счетчика цикла играет переменная i, которая должна в цикле изменяться от 1 до N. Поскольку шаг явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6.
Сразу после входа в цикл переменная i примет начальное значение i = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к. i = 1). Если этот элемент действительно положителен, то в блоке б он будет добавлен к переменной S, после чего выполняется возврат к заголовку цикла. Если этот элемент не положителен (т. е. нуль или отрицательный), то будет выполнен переход сразу к заголовку цикла, минуя блок суммирования 6.
На втором круге цикла счетчик i в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и, если он положителен, то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N. При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N+1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 7. В этом блоке выводится накопленная сумма и алгоритм закончит работу.
Источник
Алгоритмы циклической структуры



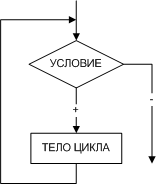
Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 3 изображен цикл с предусловием, а на рис. 4 — цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями.
· в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием — после тела цикла;
· в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;
· в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием — условие выхода из цикла.
| FOR I=A TO B [ STEP C ] | FOR I:=A B DO |
| P | P; |
| NEXT I | |
| WHILE | WHILE DO |
| P | |
| DO | REPEAT |
| P | P; |
| LOOP UNTIL Q | INTIL ; |
 |
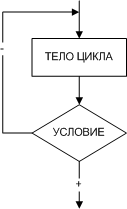 |
| Рис. 3. Алгоритм циклической структуры с предусловием | Рис. 4. Алгоритм циклической структуры с постусловием |
При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.
Кроме того, существует так называемый безусловный циклический алгоритм (рис. 5), который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла.
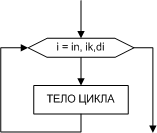 |
| Рис. 5. Алгоритм циклической структуры без условия |
Выполнение безусловного циклического алгоритма начинается с присвоения переменной i стартового значения in. Затем следует проверка, не превосходит ли переменная i конечное значение iк. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная i меняет свое значение в соответствии с указанным шагом di. Далее, снова производится проверка значения переменной i и алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным. Например, так как показано на рис. 6.
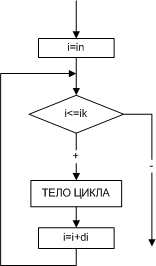 |
| Рис. 6. Условный циклический алгоритм с известным числом повторений |
Отметим, что переменную i называют параметром цикла, так как это переменная, которая изменяется внутри цикла по определенному закону и влияет на его окончание.
Рассмотрим использование алгоритмов циклической структуры на конкретных примерах.
ПРИМЕР 4. Найти наибольший общий делитель (НОД) двух натуральных чисел А и В.
Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в таблице 2.
| Таблица 2. Поиск НОД для чисел А=25 и В=15. | ||||
| Исходные данные | Первый шаг | Второй шаг | Третий шаг | НОД(А,В)=5 |
| А=25 | А=10 | А=10 | А=5 | |
| В=15 | В=15 | В=5 | В=5 |
В блок-схеме решения задачи, представленной на рис. 2.5, для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В.
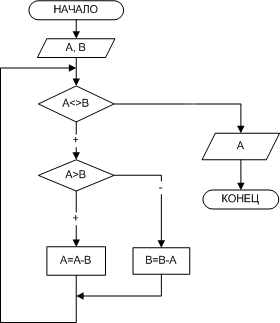 |
| Рис. 7. Поиск наибольшего общего делителя двух чисел |
ПРИМЕР 2.2. Вводится последовательность чисел, 0 — конец последовательности. Определить, содержит ли последовательность хотя бы два равных соседних числа.
Входные данные:x0 — текущий член последовательности, x1 — следующий член последовательности.
Выходные данные: сообщение о наличии в последовательности двух равных соседних элементов.
Вспомогательные переменные: Fl — логическая переменная, сохраняет значение «истина», если в последовательности есть равные рядом стоящие члены и «ложь» — иначе.
Блок-схема решения задачи приведена на рис.7. Применение здесь цикла с постусловием обосновано тем, что необходимо вначале сравнить два элемента последовательности, а затем принять решение об окончании цикла.
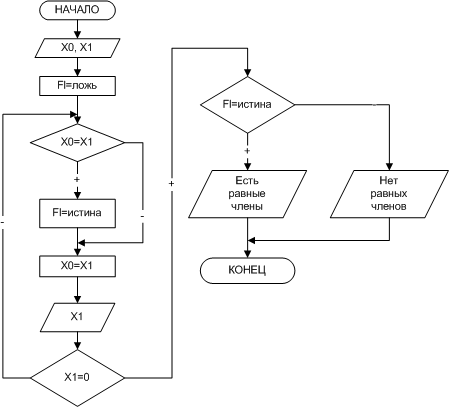 |
| Рис. 7. Поиск равных соседних элементов последовательности |
В приведенных примерах условие задачи таково, что неизвестно, сколько раз повторится тело цикла. Такие циклы называют циклами с неизвестным числом повторений (вообще говоря, неизвестно, закончится ли цикл вообще). Цикл, количество повторений которого известно заранее или его можно определить по исходным данным, называют циклом с известным числом повторений.
Рассмотрим несколько примеров с использованием таких циклов.
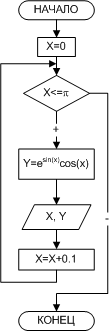
ПРИМЕР 7. Составить таблицу значений функции y = e sin(x) cos(x) на отрезке [0;π] с шагом 0.1.
Входные данные: начальное значение аргумента — 0, конечное значение аргумента — π , шаг изменения аргумента — 0.1.
Выходные данные: множество значений аргумента X и соответствующее им множество значений функции Y.
 |
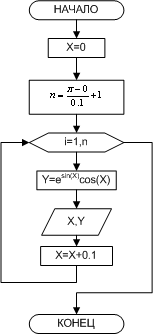 |
| Рис. 7. Создание таблицы значений функции y = e sin(x) cos(x) (1-й способ) | Рис. 8. Создание таблицы значений функции y = e sin(x) cos(x) (2-й способ) |
В условии задачи количество повторений цикла явно не задано, поэтому решить ее можно, используя цикл с предусловием (рис. 2.7). С другой стороны известно, как изменяется параметр цикла X и каковы его начальное и конечное значения, следовательно, предварительно определив количество повторений тела цикла n, так как показано на рис. 2.8, можно воспользоваться безусловным циклическим оператором. Итак, если параметр цикла X принимает значения в диапазоне от xn до xk, изменяясь с шагом dх, то количество повторений тела цикла можно определить по формуле:
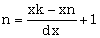 |
округлив результат деления до целого числа.
ПРИМЕР 8. Вычислить факториал числа N (N!=1 2 3 … N).
Входные данные:N— целое число, факториал которого необходимо вычислить.
Выходные данные:factorial— значение факториала числа N, произведение чисел от 1 до N, целое число.
Промежуточные данные:i— целочисленная переменная, принимающая значения от 2 до N с шагом 1, параметр цикла. Блок-схема приведена на рис. 9.
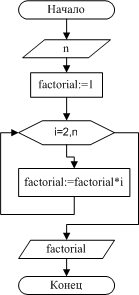 |
| Рис. 9. Вычисление факториала |
Итак, вводится число N. Переменной factorial, предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем factorial считывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается в участок памяти с именем factorial. Когда параметр i становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.
ПРИМЕР 9. Вычислить a n (n > 0).
Входные данные:a — вещественное число, которое необходимо возвести в целую положительную степень n.
Выходные данные:p (вещественное число) — результат возведения вещественного числа a в целую положительную степень n.
Промежуточные данные:i— целочисленная переменная, принимающая значения от 1 до n с шагом 1, параметр цикла.
Блок-схема приведена на рис. 2.10.
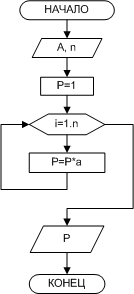 |
| Рис. 10. Возведение вещественного числа в целую степень |
Известно, что для того, чтобы получить целую степень n числа a, нужно умножить его само на себя n раз. Результат этого умножения будет храниться в участке памяти с именем p. При выполнении очередного цикла из этого участка предыдущее значение будет считываться, умножаться на основание степени a и снова записываться в участок памяти p. Цикл выполняется n раз.
В таблице 2.2 отображен протокол выполнения алгоритма при возведении числа 2 в пятую степень: a = 2, n = 5. Подобные таблицы, заполненные вручную, используются для тестирования — проверки всех этапов работы программы.
| Таблица 3. Процесс возведения числа a в степень n |
| i |
| P |
ПРИМЕР 10. Вычислить сумму натуральных четных чисел, не превышающих N.
Входные данные:N — целое число.
Выходные данные:S— сумма четных чисел.
Промежуточные данные:i — переменная, принимающая значения от 2 до N с шагом 2, следовательно, также имеет целочисленное значение.
При сложении нескольких чисел необходимо накапливать результат в определенном участке памяти, каждый раз считывая из этого участка предыдущее значение суммы и прибавляя к нему следующее слагаемое. Для выполнения первого оператора накапливания суммы из участка памяти необходимо взять такое число, которое не влияло бы на результат сложения. Т.е. перед началом цикла переменной, предназначенной для накапливания сумы, необходимо присвоить значение нуль. Блок-схема решения этой задачи представлена на рис. 11.
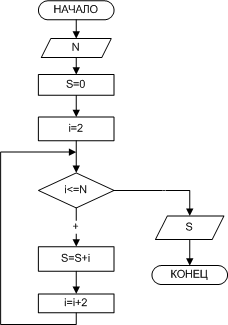 |
| Рис. 11. Вычисление суммы четных, натуральных чисел |
В таблице 3 приведены результаты тестирования алгоритма для n = 7. Несложно заметить, что при нечетных значениях параметра цикла значение переменной, предназначенной для накапливания суммы, не изменяется.
| Таблица 3. Суммирование четных чисел |
| i |
| S |
ПРИМЕР 11. Дано натуральное число N. ОпределитьК — количество делителей этого числа, не превышающих его (N = 12, его делители 1, 2, 3, 4, 6, K = 5).
Входные данные:N — целое число.
Выходные данные: целое число K — количество делителей N.
Промежуточные данные:i — параметр цикла, возможные делители числа N.
В блок-схеме, изображенной на рис. 2.12, реализован следующий алгоритм: в переменную K, предназначенную для подсчета количества делителей заданного числа, помещается значение, которое не влияло бы на результат, т.е. нуль. Далее организовывается цикл, в котором изменяющийся параметр iвыполняет роль возможных делителей числа N. Если заданное число делится нацело на параметр цикла, это означает, что i является делителем N, и значение переменной K следует увеличить на единицу. Цикл необходимо повторить N/2 раз.
В таблице 2.4 отображены результаты тестирования алгоритма при определении делителей числа N = 12.
| Таблица 2.4. Определение делителей числа N |
| i |
| K |
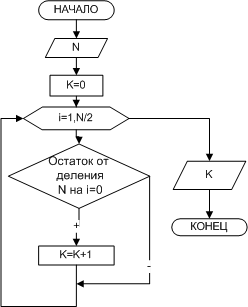 |
| Рис. 12. Определение делителей натурального числа |
ПРИМЕР 12. Дано натуральное число N. Определить, является ли оно простым. Натуральное число N называется простым, если оно делится нацело без остатка только на единицу и N. Число 13 — простое, так как делится только на 1 и 13, N = 12 не является простым, так как делится на 1, 2, 3, 4, 6 и 12.
Входные данные:N — целое число.
Выходные данные: сообщение.
Промежуточные данные:i — параметр цикла, возможные делители числа N.
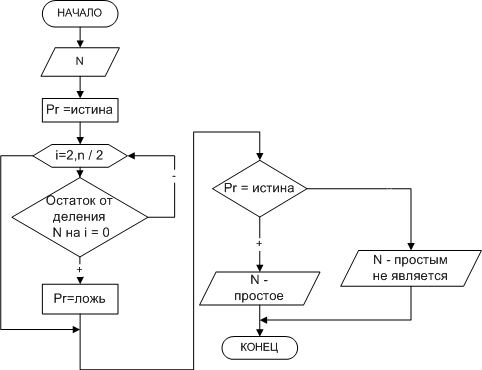 |
| Рис. 13. Определение простого числа |
Алгоритм решения этой задачи (рис. 2.13) заключается в том, что число Nделится на параметр цикла i, изменяющийся в диапазоне от 2 до N/2. Если среди значений параметра не найдется ни одного числа, на которое заданное число N делится нацело, то N — простое число, иначе оно таковым не является. Обратите внимание на то, что в алгоритме предусмотрено два выхода из цикла. Первый — естественный, при исчерпании всех значений параметра, а второй — досрочный. Нет смысла продолжать цикл, если будет найден хотя бы один делитель из указанной области изменения параметра.
ПРИМЕР 13. Определить количество простых чисел в интервале от N до M, где N и M — натуральные числа.
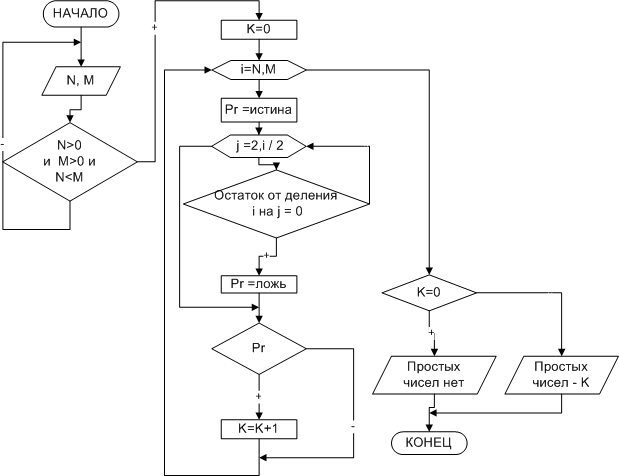 |
| Рис. 14 Поиск простых чисел в заданном интервале |
ПРИМЕР 14. Вычислить значения y, соответствующие каждому значению x (xn ≤ x ≤ xk, dx) по формуле:
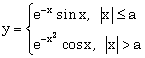 |
Найти максимальное и минимальное значение у.
Входные данные:xn, xk, dx, a.
Выходные данные: множество значений у, ymax— максимальное значение у, ymin — минимальное значение у.
Алгоритм поиска минимального (максимального) значения переменной у можно описать следующим образом. Пусть минимальное (максимальное) значение y хранится в переменной ymin (ymax). До начала цикла этой переменной присваивается очень большое (маленькое) значение, например, 10 20 (-10 20 ). Затем в цикле сравниваются значения y и ymin (ymах), и если встречается значение у меньшее (большее), чем хранится в ymin (ymах), то его необходимо записать в переменную ymin (ymах). Таким образом, все значения у неявно сравниваются между собой, а по окончании цикла в переменной ymin (ymах) будет храниться наименьшее (наибольшее) среди значений у.
Блок-схема алгоритма изображена на рис. 15.
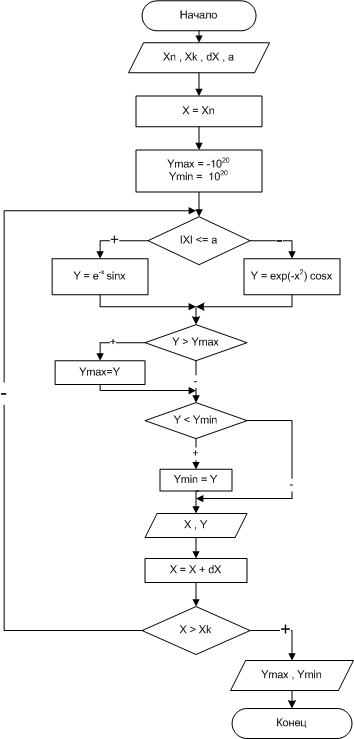 |
| Рис. 15. Блок-схема алгоритма примера 10 |
ПРИМЕР 16. Вычислить значения z, которые соответствуют каждому значению х (x = 1; dx = 0.5) по формуле:
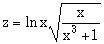 |
Считать z до тех пор, пока подкоренное выражение больше или равно 0,02. Определить k — количество вычисленныхz.
Входные данные:x, dx.
Выходные данные: множество значений z , k — количество вычисленныхz.
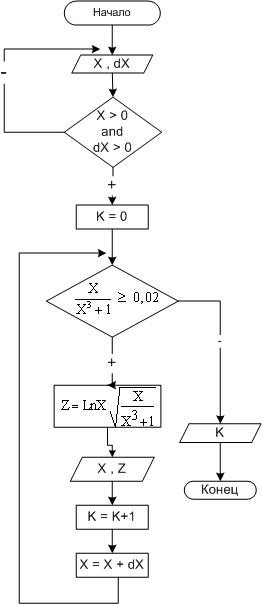
Здесь условие окончания цикла явно указано в условии примера. Цикл окончится, когда подкоренное выражение станет меньше 0,02. Блок-схема алгоритма изображена на рис. 2.16.
 |
 |
| Рис. 16. Блок-схеме алгоритма примера 2.11 | Рис. 17. Блок-схема алгоритма примера 2.12 |
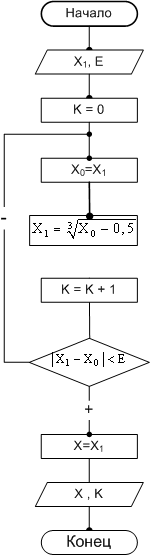
ПРИМЕР 17. Вычислить отрицательный корень уравнения x 3 — x + 0,5=0, используя рекуррентную формулу:
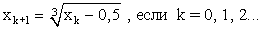 |
и если x0= -1,3; ε =10 -4 . Определить количество итераций (шагов цикла); вычисления прекратить при выполнении условия │xk+1 — xk│ -4 .
Входные данные:U — начальное приближение, х, E— точность (ε).
Выходные данные:y — значение вычисленной функции, k — количество итераций.
Блок-схема алгоритма изображена на рис. 2.18.
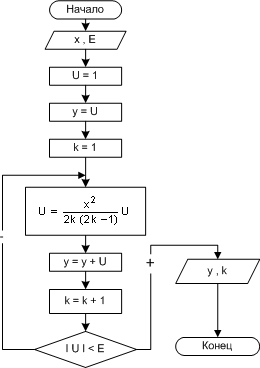 |
| Рис. 18. Блок-схема алгоритма примера 18 |
В отличие от предыдущего примера, здесь достаточно одной переменной U, в которой будет храниться текущее значение у. На каждом шаге циклического алгоритма необходимо пересчитывать значение у и к нему добавлять U. Цикл окончится, когда абсолютное значение U станет меньше E. По окончании цикла выводится y — сумма значений U.
ПРИМЕР 19. Вводится последовательность целых чисел, 0 — конец последовательности. Найти минимальное среди положительных, если таких значений несколько, определить, сколько их.
Блок-схема решения задачи приведена на рис. 19.
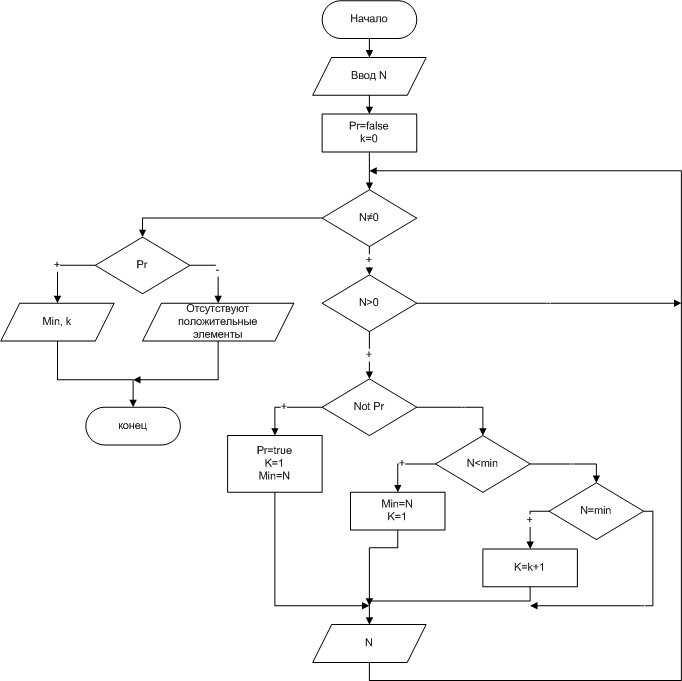 |
| Рис. 19. Блок-схема нахождения минимального положительного числа последовательности |
При решении этой задачи используется логическая переменная Pr, которая определяет наличие положительных чисел в последовательности (Pr = false, если положительных чисел нет). Основной цикл работает до тех пор, пока N ≠ 0. При каждом входе в цикл проверяем, знак N. Если N> 0, а pr = false, то это говорит о том, что это первое положительное число. В этом случае это число объявляем минимальным, количество минимальных чисел (k) равным 1, а признак pr = true. Если N > 0, а pr не равно false, то сравниваем текущее значение N с min. Если N

Источник
