Комбинационными схемами называют логические схемы, у которых выходные сигналы в каждый момент времени однозначно определяются комбинацией входных сигналов в тот же момент времени, т.е. не зависят от предыстории процесса. Проще говоря, комбинационная схема не обладает памятью.
Поведение комбинационной схемы в статическом режиме (без учёта задержки распространения сигнала) описывается функциями алгебры логики, которые на практике задаются как в алгебраической форме, так и в виде таблицы истинности.
При работе с комбинационными схемами возникают задачи анализа и синтеза.
Задача анализа состоит в определении статических и динамических свойств заданной комбинационной схемы. В статике определяются логические функции, реализуемые комбинационной схемой. В динамике рассматривается функционирование схемы в переходных процессах при изменении значений переменных на входах схемы, т.е. определяется наличие на выходах возможных нежелательных импульсных сигналов, не предусмотренных реализуемой логической функцией.
Результаты анализа могут использоваться для определения реакции схемы на различные комбинации входных воздействий (что важно при диагностике), а также для рассмотрения работы системы, включающей в себя данную схему.
Наиболее простым способом анализа является составление таблицы истинности: для каждой комбинации входных переменных прослеживается путь от входов к выходам и определяется значение выходной переменной. Затем по таблице истинности составляется логическая функция, которая при необходимости преобразуется к наиболее удобному или компактному виду. При большом числе входов этот способ становится слишком трудоемким. В этом случае проще использовать алгебраический подход, который заключается в том, что непосредственно по схеме, переходя от входов к выходам, составляется логическое выражение, отображающее все операции, выполняемые логическими элементами.
Задача синтеза заключается в построении из заданного набора логических элементов комбинационной схемы, реализующей заданную систему логических функций. Эта задача возникает при разработке логических устройств. Ее решение не является однозначным: одну и ту же систему логических функций можно реализовать множеством вариантов комбинационных схем, отличающихся по тем или иным параметрам. Разработчик из этого множества вариантов выбирает один исходя из дополнительных критериев: минимального количества использованных логических элементов, максимального быстродействия и т.д.
Описание работы комбинационной схемы обычно вначале формулируется на естественном языке. Далее необходимо формализовать задачу. Наиболее простой и наглядный путь формализации – составление таблицы истинности, исходя из которой логическая функция записывается в алгебраической форме. После этого логическая функция минимизируется и преобразуется к виду, наиболее удобному для реализации. На последнем этапе производится выбор элементной базы и составляется принципиальная электрическая схема устройства.
Бывает, что подлежащая реализации логическая функция задана не на всех возможных наборах аргументов. Тогда на тех наборах, где функция не определена, ее доопределяют так, чтобы в результате минимизации получить наиболее простое выражение, что упростит и саму схему.
Рассмотрим пример. Пусть необходимо построить мажоритарную ячейку (называемую также схемой голосования) на три входа. Сигнал на выходе ячейки принимает значение, присутствующее на большинстве входов.
Заполняем таблицу истинности (табл. 4.4). При трех входных сигналах x1, x2 и x3 возможно восемь различных комбинаций значений. Удобно воспринимать входные переменные как разряды двоичного числа, тогда каждой комбинации соответствует число N.
Пользуясь табл. 4.4, легко записать выходную логическую функцию y(x1, x2, x3) в виде совершенной дизъюнктивной нормальной формы (СДНФ). СДНФ представляет собой дизъюнкцию конъюнкций, содержащих все переменные (с отрицанием или без). Конъюнкции записываются для тех строк таблицы, в которых y = 1, при этом если соответствующий аргумент принимает в строке значение 0, он входит в конъюнкцию с отрицанием, а если 1 – без отрицания. В данном случае
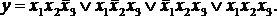(4.1)
Целью минимизации является получение алгебраического выражения, содержащего минимальное количество символов переменных, исходя из того, что при этом и реализующая схема будет наиболее простой. Вид выражения (4.1) несложен, поэтому минимизацию можно выполнить с использованием основных тождеств алгебры логики, приведенных в п. 4.1. Например, возможно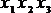 
представить как 
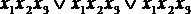, а затем перегруппировать слагаемые:
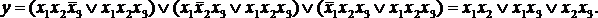
Как видим, окончательное выражение значительно проще исходного. Полученная форма является дизъюнктивной нормальной формой (ДНФ). В данном случае это минимальная ДНФ.
Дальнейшее преобразование определяется тем, какие логические элементы выбраны для реализации. Если допустимо использовать ЛЭ И и ИЛИ, то структура схемы будет непосредственно повторять структуру формулы (рис. 4.6, а). Если же выбран один из наиболее распространенных логических элементов – И-НЕ, то необходимо преобразовать полученную минимальную ДНФ с помощью правила де Моргана:
 |
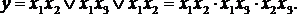
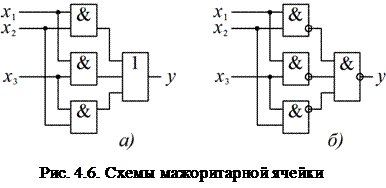Реализация последнего выражения показана на рис. 4.6, б.
В случае более сложной исходной СДНФ минимизация при помощи алгебраических преобразований неочевидна, ее результат зависит от квалификации специалиста. Для функций, содержащих не более 5-6 аргументов, существует наглядный способ минимизации при помощи карт Карно (называемых также диаграммами Вейча). Способ гарантирует получение наиболее простого конечного выражения.
Карта Карно представляет собой прямоугольную таблицу, каждой клетке которой ставится в соответствие определенная конъюнкция, причем это делается таким образом, чтобы конъюнкции в соседних клетках отличались не более чем на один сомножитель. При заполнении таблицы в соответствующую клетку ставится 1, если минимизируемая функция при данном наборе аргументов равна единице. В остальные клетки вписываются нули (хотя для упрощения их можно оставить пустыми).
Табл. 4.5 представляет собой карту Карно для функции, представленной в табл. 4.4. Каждой строке соответствует одна переменная, каждому столбцу – две переменных. Конъюнкция, соответствующая каждой клетке, образуется из переменных столбца и строки, на пересечении которых расположена клетка.
| x2 |
x2 |
 x2 |
x2 |
| x1 | |||
| x1 | |||
| x3 | x3 |
x3 |
x3 |
В заполненной таблице покрывают прямоугольными контурами все единицы. Контуры могут включать 1, 2, 4, 8… клеток, при этом условии каждому контуру соответствует определенная конъюнкция. Минимизированная функция записывается в виде дизъюнкции конъюнкций, соответствующих контурам.
При проведении контуров придерживаются следующих правил:
─ контур должен быть прямоугольным;
─ внутри контура должны быть только клетки, заполненные единицами;
─ число клеток, покрытых контуром, может быть равно 1, 2, 4, 8…;
─ количество контуров должно быть как можно меньшим, а сами контуры – как можно больше;
─ крайний левый и крайний правый столбцы считаются соседними, как если бы карта была свернута в виде цилиндра, точно так же в карте с большим числом строк верхняя и нижняя строки считаются соседними;
─ каждая единица может быть покрыта несколько раз.
После покрытия всех единиц записывается минимизированная функция. При записи конъюнкции, соответствующей некоторому контуру, в нее включают только те аргументы, которые не изменяют своего значения внутри контура. Так, в один из контуров табл. 4.5 входят клетк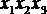и 
и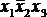 
. Значит, этому контуру приписывается значение 
.
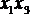Легко убедиться, что, записав дизъюнкцию конъюнкций всех трех контуров, использованных в табл. 4.5, получим то же выражение, что и полученное ранее алгебраическим путем.
В ряде случаев может существовать несколько вариантов покрытия единиц прямоугольниками. Это означает, что задача минимизации не обязательно имеет единственное решение: различные по записи функции могут иметь одинаковые таблицы истинности и быть равноправными с точки зрения минимальности ДНФ.
| Таблица 4.6 | |||
 |
|
 |
|
 |
 |
||
 |
|
||
|
 |
||
|
|
||
 |
 |
|
|
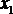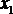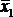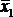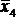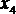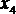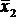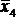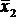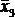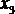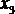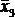Карта Карно для функции четырех переменных представлена в табл. 4.6. Надо отметить, что существует множество способов разметки строк и столбцов карты; главное требование – чтобы соседние строки, равно как и соседние столбцы, отличались друг от друга значением только одной переменной. Поэтому табл. 4.6 представляет собой один из возможных вариантов. Для облегчения заполнения удобно пронумеровать клетки карты так же, как строки таблицы истинности. В табл. 4.6 принято для нумерации, что двоичное число имеет вид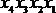 
(x1 – младший разряд).
| Таблица 4.7 | |||||
| N | x4 | x3 | x2 | x1 | y |
Используем табл. 4.6 для синтеза логической цепи, определяющей степень близости двух двухразрядных двоичных чисел 
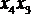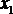и 
( и 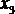– младшие разряды). Пусть функция y будет равна единице, если 
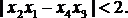Таблица истинности такой функции приведена в табл. 4.7. В зависимости от способа покрытия клеток с номерами 6 и 9 существует четыре варианта записи минимальной ДНФ. Один из них имеет вид:
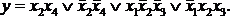
Предлагается читателю в качестве самостоятельного упражнения найти еще три варианта и убедиться, что таблицы истинности всех функций совпадают.
Более сложно выглядит синтез комбинационной схемы, описываемой системой логических функций (иначе говоря – если комбинационная схема имеет несколько выходов). При каноническом методе синтеза предполагается, что каждая выходная функция реализуется своей схемой. Поэтому синтез сложной схемы с n выходами заменяется синтезом n схем с одним выходом. Однако оптимизация каждой логической функции в отдельности, как правило, не дает оптимального результата в целом.
Рассмотрим пример. Пусть требуется реализовать систему логических функций
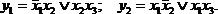(4.2)
Реализация непосредственно по представленным выражениям показана на рис. 4.7, а. Сложность полученной схемы можно оценить либо по суммарному числу входов nвх всех логических элементов, либо про числу корпусов nк интегральных микросхем. При определении nк принимается типичный для микросхем малой степени интеграции состав ЛЭ: в одном корпусе шесть одновходовых, или четыре двухвходовых, или три трехвходовых, или два четырехвходовых ЛЭ. Для схемы рис. 4.7, а nвх = 14; nк = 11/6. Если представить систему (4.2) в эквивалентной форме
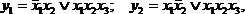(4.3)
 |
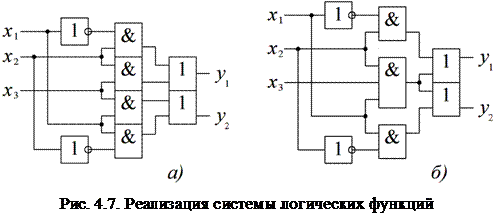то их реализация (рис. 4.7, б) характеризуется параметрами: nвх = 13; nк = 5/3. Выигрыш достигается за счет того, что конъюнкция x1x2x3 реализуется один раз, а участвует в формировании обеих функций.
Иногда выгодно использовать каскадное соединение ЛЭ. Существует понятие порядок логической функции – это максимальное число последовательно выполняемых операций. При непосредственной реализации функции по ее выражению это означает максимальное число последовательно включенных логических элементов. Так, функция в любой нормальной форме имеет порядок 2. При вынесении за скобки порядок увеличивается.
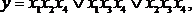(4.4)
имеющую порядок 2. После вынесения за скобки она принимает вид:
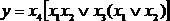(4.5)
 |
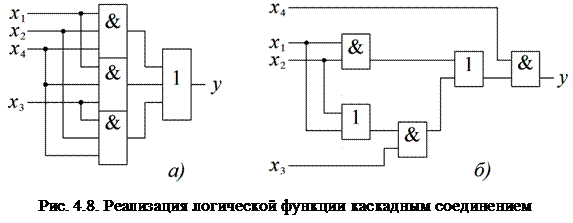с порядком 4. Реализация функций по выражениям (4.4) и (4.5) показана соответственно на рис. 4.8, а (nвх = 12; nк =4/3) и 4.8, б (nвх = 10; nк =5/4). Видно, что каскадное соединение упрощает схему, зато ухудшает быстродействие за счет того, что увеличивается общая задержка распространения сигнала.
Реализация логических функций, представленная на рис. 4.6 – 4.8, выполнена традиционным способом: с использованием простейших ЛЭ. Однако современная электроника позволяет коренным образом изменить подход к реализации цифровых устройств, поскольку в состав развитых серий цифровых ИМС входит множество типовых комбинационных схем, и необходимо лишь наиболее полно использовать их функциональные возможности. В частности, мультиплексоры (см. п. 4.5) позволяют реализовывать произвольные логические функции непосредственно по таблице истинности, не используя минимизацию.
Источник