Построение логических схем
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнить арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
Алгоритм построения логических схем :
1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль.
4) Соединить вентили в порядке выполнения логических операций.
Составить логическую схему для логического выражения: F = ¬ X v Y & X .
2) Две логические операции: 1 3 2
3) Строим схему, соединяя вентили в порядке выполнения логических операций:
Постройте логическую схему, соответствующую логическому выражению F = X & Y v ¬ ( Y v X ).
Вычислить значения выражения для X =1, Y =0.
2) Логических операций четыре: конъюнкция, две дизъюнкции и отрицание. Определяем порядок выполнения операций:
3) Схему строим слева направо в соответствии с порядком выполнения логических операций:
4) Вычислим значение выражения: F =1&0 v ¬ ( 0 v 1)=0.
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:
1) F=A v B& ¬ C, если A=1, B=1, C=1 .
2) F = ¬ (A v B&C), если A=0, B=1, C=1 .
3) F = ¬ A v B&C, если A=1, B=0, C=1 .
4) F =(A v B)&(C v B), если A=0, B=1, C=0 .
7) F= ¬ (A&B&C) v (B&C v ¬ A), если A=1, B=1, C=0 .
Источник
Составление таблиц истинности для логических высказываний нескольких переменных
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
При составлении таблицы истинности для логического выражения необходимо учитывать порядок выполнения логических операций , а именно:
Алгоритм составления таблицы истинности :
1. Выяснить количество строк в таблице (вычисляется как 2 n , где n – количество переменных + строка заголовков столбцов).
2. Выяснить количество столбцов (вычисляется как количество переменных + количество логических операций).
3. Установить последовательность выполнения логических операций.
4. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
5. Заполнить таблицу истинности по столбцам.
Построим таблицу истинности для выражения F =( Av B )&( ¬ A v ¬ B ) .
1. Количество строк=2 2 (2 переменных+строка заголовков столбцов)=5.
2. Количество столбцов=2 логические переменные (А, В)+ 5 логических операций ( v ,&, ¬ , v , ¬ ) = 7.
3. Расставим порядок выполнения операций: 1 5 2 4 3
4-5. Построим таблицу и заполним ее по столбцам:
6. Ответ: F =0, при A= B=0 и A= B=1
Построим таблицу истинности для логического выражения F = X v Y & ¬ Z .
1. Количество строк=2 3 +1=(3 переменных+строка заголовков столбцов)=9.
2. Количество столбцов=3 логические переменные+3 логических операций = 6.
3. Укажем порядок действий: 3 2 1
4-5. Построи м таблицу и заполним ее по столбцам:
6. Ответ: F =0, при X= Y= Z= 0; при X= Y=0 и Z= 1.
Постройте таблицы истинности для следующих логических выражений:
Наборы входных переменных, во избежание ошибок, рекомендуется перечислять следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
Тавтология — тождественно истинная формула , или формула принимающая значение » истина » (» 1 «) при любых входящих в нее значениях переменных.
Противоречие — тождественно ложная формула , или формула принимающая значение » ложь » (» 0 «) при любых входящих в нее значениях переменных.
Равносильные формулы — две формулы А и В принимающие одинаковые значения, при одинаковых наборах значений входящих в них переменных. Равносильность двух формул алгебры логики обозначается символом .
Источник
Таблица истинности
Инструкция . При вводе с клавиатуры используйте следующие обозначения:
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ ( |
bc необходимо ввести так: a*b*c+a*b=c+a=b*c Для ввода данных в виде логической схемы используйте этот сервис.
Для булевой функции, заданной вектором значений (например, 00111011 ) используйте ввод данных через таблицу.
Правила ввода логической функции
- Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
- Перед логической функцией не надо указывать обозначение функции. Например, вместо F(x,y)=(x|y)=(x^y) необходимо ввести просто (x|y)=(x^y) .
- Максимальное количество переменных равно 10 .
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
Источник
Презентация «Логические схемы» 10 класс
Код для использования на сайте:
Скопируйте этот код и вставьте себе на сайт
Для скачивания поделитесь материалом в соцсетях
После того как вы поделитесь материалом внизу появится ссылка для скачивания.
Подписи к слайдам:
Построение логических схем
- Определить число логических переменных.
- Определить количество базовых логических операций и их порядок.
- Изобразить для каждой логической операции соответствующий вентиль.
- Соединить вентили в порядке выполнения логических операций.
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
Представить в виде логической схемы логическую формулу:
Логическая схема будет выглядеть так:
Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1, B=0
В результате получится логический ноль, т.е. «ложно».
Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1.
Читать эту схему надо слева направо. Первой выполняется операция И (что наглядно видно на схеме), затем ИЛИ.
Теперь в порядке слева направо припишем к выходящим линиям результаты операций:
В результате получилась 1, т.е. «истина».
Составить логические выражения по схемам:
а) НЕ((В И С) ИЛИ НЕ(А)) б) (А И В) ИЛИ НЕ В) ИЛИ НЕ (А ИЛИ В)
Составьте таблицы истинности для следующих логических выражений:
Постройте логическое выражение по логической схеме:
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:
F = AvB& C, если А = 1, В=1, С=1 (1).
F = (AvB) & (CvB), если А=0, В=1, С=0 (1).
F = ¬ (A&B&C) v (B & C vA), если А=1, В=1, С=0 (1).
I. Упростите логические выражения:
II. Дана следующая логическая схема. Упростите ее, используя минимальное количество вентилей.
III. Как составить расписание.
При составлении расписания учителя высказали следующие пожелания: учитель физики хочет иметь первый и второй урок; учитель химии — первый или третий; учитель информатики — второй или третий. Предложите возможные варианты расписания.
Список литературы:
- Н.Угринович “Информатика и информационные технологии” 10-11 класс. Издательство Москва Бином. Лаборатория знаний. 2015 г.
- Н.Угринович, Л.Босова, Н.Михайлова “Практикум по информатике и информационным технологиям” Издательство Москва Бином. Лаборатория знаний. 2015 г.
- О.Л.Соколова “Поурочные разработки по информатике” Москва “ВАКО” 2014 г.
Источник
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику




 Практическая работа №5,6
Практическая работа №5,6
Тема: Логические величины, операции, выражения. Построение логических схем.
Цель работы: научиться составлять аналитические выражения по табличному значению функции, строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.
особенности применения логических элементов;
производить синтез и анализ аналитических выражений логических функций
строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.
Функция отрицание НЕ или инверсия
Таблица истинности функции отрицания имеет вид:
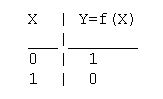
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
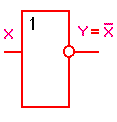
Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2
Таблица истинности логического ИЛИ имеет вид:
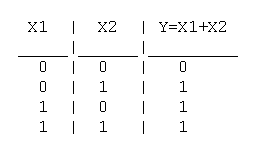
Логический элемент ИЛИ обозначается на схемах следующим образом:
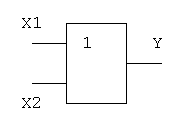
Логическое И (логическое умножение, конъюнкция ): Y = X1X2 = X1&X2
Таблица истинности логического И имеет вид:
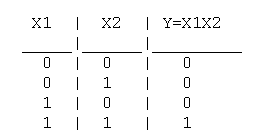
Логический элемент И обозначается на схемах следующим образом:
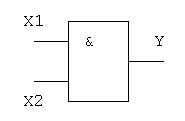
Таблица истинности функции ИЛИ-НЕ имеет вид:
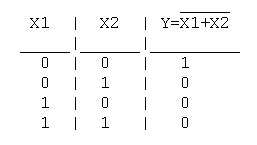
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:
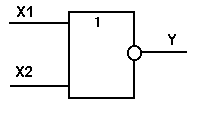
Таблица истинности функции И-НЕ имеет вид:
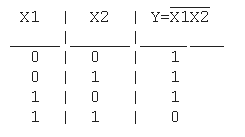
Логический элемент И-НЕ обозначается на схемах следующим образом:
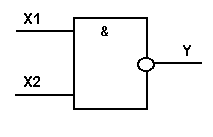
2. Алгоритм построение логических схем.
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.
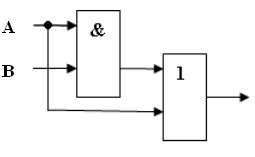
Пример 1.
Составить логическую схему для логического выражения: F=A v B & A. Две переменные – А и В.Две логические операции: 1-&, 2-v.
Строим схему:
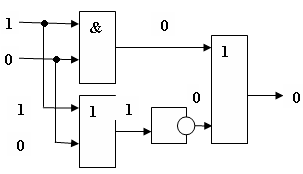
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0. Переменных две: А и В; Логических операций три: & и две v; А&Вv (Вv А).Схему строим слева направо в соответствии с порядком логических операций:
3. Составление аналитического выражения функции и построение логической схемы по табличному заданию функции.
Синтез комбинационных устройств может быть произведен по табличному заданию функции по «0» и «1». Рассмотрим для примера синтез по «1». Для всех значений аргументов х 1 , х 2 , х 3 , где функция задана как «1» берется их конъюнкция, если аргумент равен «1», если же 0 – конъюнкция их инверсий. От полученных конъюнкций берется дизъюнкция.
Например, функция от трех аргументов задана следующей таблицей:
Источник

Вам также может понравиться
